Last Week

• Unsupervised Machine Learning
  • Clustering with k-means
  • Dimensionality Reduction with PCA

This Week

• Supervised Machine Learning
  • In depth: Decision Trees
• Ensemble Methods
  • Forests
  • Meta-Learners
• Optimising Your Model
  • Cross Validation Methods
  • Hyperparameter Tuning

Supervised Learning: Use X to infer Y

• Supervised Learning starts with a dataset containing both features (\(X\)) and labels (\(y\)).
• They then construct a “rule” relating \(X\) to \(y\), so that given some combination of values for \(X\), they can “predict” a value of \(y\).
• In other terms, supervised learning finds \(f\) in \(y=f(X)\).
  • If \(y\) is discrete/categorical, then the task is called classification.
  • If \(y\) is continuous, then the task is called regression.

Supervised Learning Models

Some general classes of supervised models include:

• Linear Models
• Support Vector Machines (SVMs)
• Naive Bayes
• Tree-based Estimators
• (Supervised) Neural Networks

Decision Trees

Although radically distinct to linear estimators such as OLS, decision trees offer a simple and intuitive approach to estimating values of \(y\) based on \(X\).

• If you have played the game twenty questions, then you should be familiar with the idea behind decision trees.
• Constructs a series of binary questions (nodes) regarding your features, and eventually at the end of the resulting branches gives a prediction (leaf) of your label.

Understanding Decision Trees

A decision tree can be understood as a mapping from the multi-dimensional feature space, \(X_{ij}\), to the label space \(y_i\).

• Each question partitions the \(X_{ij}\)-space.
• Each leaf maps one of these partitions to a value (or range) in the \(y\)-space.
• The algorithm necessarily sets some convergence threshold so that there are fewer leafs than observations.

Impurity

• Given that the algorithm knows the values of \(y\):
  • Its goal is to split the \(X\)-space in such a way that each partition does not contain more than one distinct value of \(y\).
  • In essence, it wants to split the \(X\)-space in way that increases the “purity” of each partition.
  • A partition containing more than one distinct value of \(y\) will necessarily lead to at least one erroneous prediction.
• There are various measures of impurity:
  • GINI: \(H(X_m) = \sum_k p_{mk} (1 - p_{mk})\)
  • Entropy: \(H(X_m) = - \sum_k p_{mk} \log(p_{mk})\)

Visualising Trees

Tree Trade-offs

Advantages:

• Excels at capturing conditional dependencies
• Arguably more intuitive than OLS.
• Provides an metric of feature importance that has a substantive interpretation.

• Extremely prone to over-fitting.
• Does not provide a linear marginal effect estimate.

Choosing Your Supervised Algorithm

These are some of the criteria you may want to consider when choosing an algorithm:

• Prediction Accuracy: Algorithms vary in their ability to predict unseen data. We will discuss this more during cross validation.
• Minimum Data: Some models are able to do more with less. This is especially true if the model makes certain parametric assumptions about the nature or distribution of the data.
• Interpretability: Not all methods provide insight into how they formulate their predictions. Methods range from extremely intuitive, such as decision trees, to complete black boxes, such as neural networks. When seeking to explain and not predict, one should take this into account.

This brings me to…

Managing Shortcomings by Working Together

• There is no single model or algorithm that performs best across all criteria in all scenarios.
• Ensemble methods, which is really a fancy way of saying using more than one method, are often devised to address this issue.
• I group ensemble methods into two types: aggregating and sequential ensembles.
  • Aggregating Ensembles train on and estimate predicted values of the same data, and then use a meta-learner to aggregate these predictions.
  • Sequential Ensembles use the output of one algorithm (often unsupervised) as features to train another. PCA+kmeans is an example of this.

Aggregating Trees: Random Forests

There are various algorithms that aggregate decision trees, but here I outline the logic behind the most straightforward and common one: Random Forests (RFs).

• Construct \(N\) decision trees.
• For each split in each tree, randomly select a subset of features. This split can only be made over these features.
• To predict, the same input array is passed to all the constituent trees, and the algorithm either returns mean prediction (continuous data) or modal prediction (categorical data).
• The noteworthy improvement on this algorithm is Bayesian Additive Regression Trees (BARTs).

Aggregating Learners: Meta-Learners

A number of papers have been published recently that use ensemble methods to estimate heterogeneous treatment effects:

• Grimmer & Westwood, Political Analysis 2017
• Kunzel et al, PNAS 2019

These papers both focus on innovating on the meta-learner.

Machine Learning is not just Algorithms

• Another contribution of machine learning to econometrics, in my opinion, has been the development of strategies to test and evaluate models.
• Epistemologically, machine learning frequently takes a more agnostic view on trying to find a specific functional specification of a theoretical model.
  • This means that the “correct” model is the one that does the best job of matching empirics, and not a particular theory.
  • The cost of this is the unsuitability of many machine learning algorithms to theory testing in the traditional econometric sense.

Cross Validation

Cross validation is one such of these strategies. It consists of dividing the data into training and test sets:

1. The model is fit using the training data: \(y_{train} = f(X_{train}) + \epsilon \rightarrow \hat{f}(X)\)
2. The fitted model is applied to the test features to generate predicted values: \(\hat{y} = \hat{f}(X_{test})\)
3. The difference between the predicted values and the test labels is used as a measure of the predictive accuracy of the model: \(\hat{e} = y_{test} - \hat{y}\)

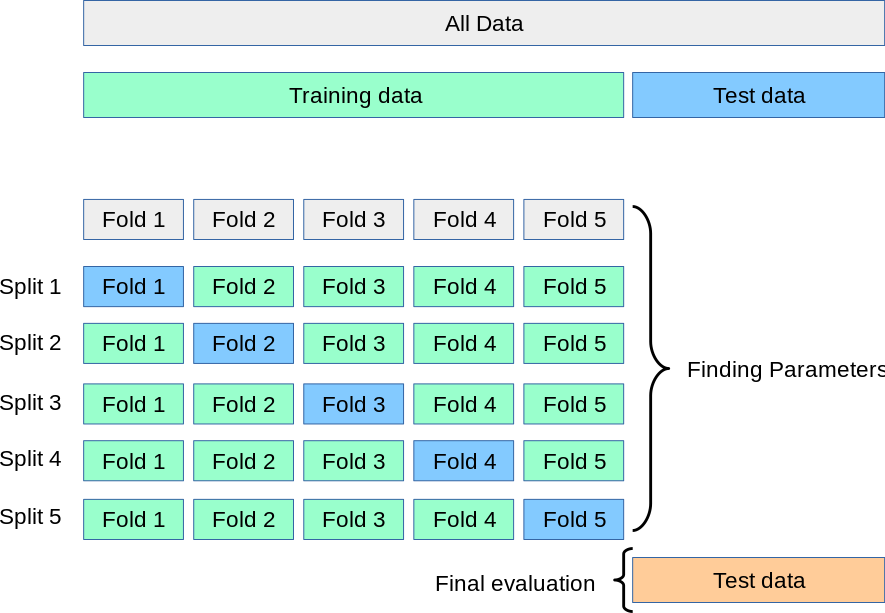
k-fold Cross Validation

• There are some obvious shortcomings to dividing the data into a training at test set just once.
• A slightly more advanced method for train-test splitting is known a k-fold CV, which consists of splitting the training data randomly into \(k\) bins, and then iteratively using the \(k\)th bin as a test set for all bins not \(k\).

Cross Validation Visualised

Choosing Parameters

Another strategy for improving the predictive accuracy of algorithms relates to choosing the right parameters.

Most, if not all algorithms have some parameters that affect predictions in very unobvious ways. For example:

• k-means: number of clusters
• Decision Tree: min/max number of splits
• Random Forest: proportion of features to use in each subset
• LASSO/Ridge/EN: \(\beta\)

Hyperparameter Tuning

• Hyperparameter tuning is the practice of choosing model parameters by maximising an objective function. Some possible objective functions include:
  • Mean Absolute Prediction Error: Combine with train-test splits.
  • Goodness-of-Fit: Measures such as R-squared, AIC, etc.
  • Coherence/Entropy Measures: Most algorithms have a measure of the complexity/information tradeoff, which can be optimised.
• Hyperparameter tuning is computationally costly, but also easily parallelisable.

Key Terms

• Unsupervised Learning: No \(y\), explore \(X\)
• Supervised Learning: Learn relationship between features and labels.
• Clustering: Split observations into groups.
• Dimensionality Redution: Reduce \(j\), the number of features.
• Classification vs Regression: Depends on structure of \(y\)
• Cross Validation: Train-test split data to optimise supervised learner.
• Hyperparameter Tuning: Systematically choose optimal parameters for algorithm.
• Objective Function: An optimisable aspect of the data used to measure goodness-of-fit.

Trade-offs

These trade-offs are not linear, but generally hold:

• Explanatory vs predictive power
• Flexibility vs efficiency
• Information vs time

Readings

Ensemble Methods:

• Grimmer & Westwood, Political Analysis 2017
• Kunzel et al, PNAS 2019

Elements of Statistical Learning:

• 9.2: Tree-Based Methods
• 15: Random Forests
• 16: Ensemble Learning